Einführung

Der Einstichproben-t-Test stellt eine einfache und grundlegende Methode dar, um einen Mittelwert mit einem fixierten Wert zu vergleichen. Gängiste Anwedungsgebiete dieses Tests liegen in Korrelations- oder Regressionsanalysen verborgen, um zu überprüfen, ob deren Koeffizienten (r, b/β) signifikant von Null verschieden sind.
Weitere Anwedungsmöglicheiten bieten sich beispielsweise an, wenn überprüft werden soll, ob sich eine Stichprobe in Bezug auf ein Merkmal einer Normstichprobe zuordnen lässt oder signifikant davon abweicht. Ebendieser Anwendungsmöglichkeit soll hier gefolgt werden.

Anwendungsbeispiel

In folgendem Beispiel soll der Test veranschaulicht werden: angenommen es wird eine Zufallstichprobe von n = 50 jugendlichen Personen gezogen. Diese Personen werden einem Leistungstest unterzogen, bei dem für erwachsene Personen ein durchschnittlicher Wert von 100 erwartet wird. Auf Basis einer A priori Poweranalyse ergibt sich eine benötigte Stichprobengröße von n = 45, um bei einem einseitigen Test eine Effektstärke von d = .50 aufzudecken – weiter wird das Signifikanzniveau auf α = .05 und die Teststärke auf 1 – β = .95 festgesetzt (beispielhafte Angaben). Es wird, nach der Konvention von Cohen (1988), ein mittlerer Effekt erwartet.

Außerdem werden folgende Hypothesen aufgestellt:

Inhaltlich:

H₀: Jugendliche Personen sind höchstens so leistungsfähig wie erwachsene Personen.

H₁: Jugendliche Personen sind leistungsfähiger als erwachsene Personen.

Statistisch:

H₀: μ ≤ 100

H₁: μ > 100

Download Beispiel-Datei: Einstichproben-t-Test.

Voraussetzungen

Stetigkeit

Das Merkmal muss in der zu grundeliegenden Population mindestens intervallskaliert und stetig sein.

Statistische Ausreißer

Der Umgang mit statistischen Ausreißern stellt selber keine explizite Voraussetzung der Methode dar, sollte aber bedacht werden, da das arithmetische Mittel sensibel ggü. solcher Ausreißer reagiert. In extremen Fällen beinflussen Ausreßer (Extremwerte) die Verteiliung der Daten derat, dass fälschlicherweise nicht davon ausgegangen wird, dass diese normalverteilt sind.

Normalverteilung

Das Merkmal muss in der zugrunde liegenden Population normalverteilt sein.
(Siehe auch Test auf Normalverteilung.)

Prüfung auf Normalverteilung (& statistische Ausreißer) des Merkmals

Die Verteilung der Testwerte des Leistungstest in der Stichprobe wird mittels Shapiro-Wilk-Test überprüft – dieser Test sollte dem Kolmogorov-Smirnov-Test bei kleineren Stichproben (n < 100) vorgezogen werden. Das Signifikanzniveau α wird auf .25 festgelegt (vgl. Test auf Normalverteilung).
Der Shapiro-Wilk-Test kann dabei nicht direkt über eine eigene Reiterauswahl erreicht werden, sondern wird innerhalb der Explorativen Datenanalyse mitberechnet. Praktischerweise kann man sich unter dieser Option einen Boxplot ausgeben lassen. Anhand dieser Grafik lassen sich Ausreißer bzw. Extremwerte erkennen.

Syntax:

EXAMINE VARIABLES=v_1 (Variablenname)
/PLOT BOXPLOT HISTOGRAM NPPLOT
/COMPARE GROUPS
/STATISTICS NONE
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.

SPSS-Menü:

Menü -> Analysieren -> Deskriptive Statistiken -> Explorative Datenanalyse…

Nach je einem Klick auf „Weiter“ und „OK“ erscheinen im Ausgabefenster folgende Ergebnisse:

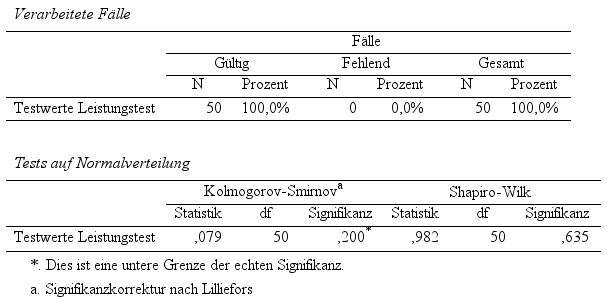
Beginnend mit einer Fallauswertung i.S.d. Anzahl der Fälle, werden nachfolgend die Ergebnisse von Kolmogorov-Smirnov- und Shapiro-Wilk-Test ausgegeben. Mit Blick auf die Spalte „Signifikanz“ des Shapiro-Wilk-Tests wird von SPSS ein Wert von p = .635 ausgegeben.
Auf Basis des Testergebnisses (p > .25),

H₀: Das Merkmal „Testwerte des Leistungstests“ ist (in der Grundgesamtheit) annähernd normalverteilt.

H₁: Das Merkmal „Testwerte des Leistungstest“ weicht (in der Grundgesamtheit) von einer Normalverteilung ab.

kann die Nullhypothese beibehalten werden. Somit kann die Voraussetzung normalverteilter Daten als gegeben angenommen werden.

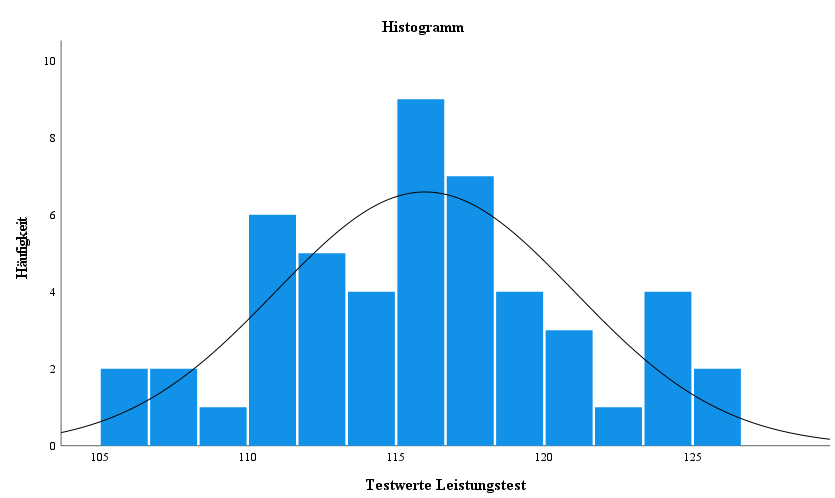
Wie auch das Testergebnis zeigt das Histogramm eine unimodale Verteilung der Beobachtungsdaten, welche vom Mittel (M = 115.98, SD = 5.04) annähernd in gleicher Weise abweichen.

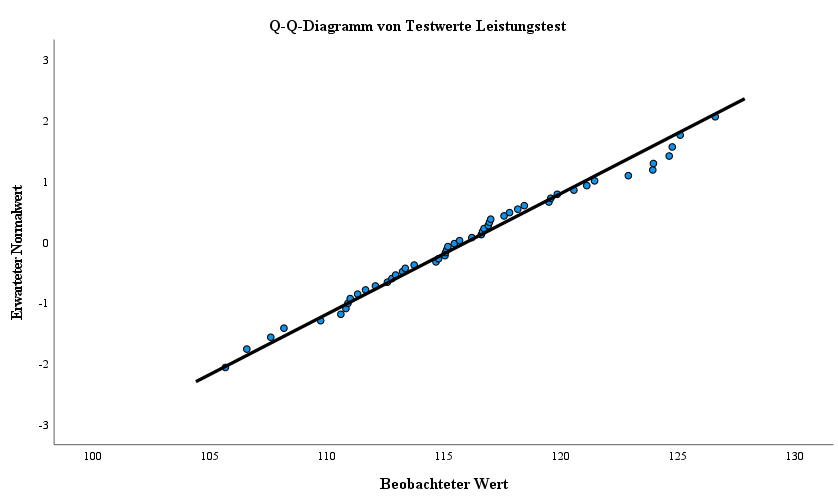
Nebenstehendes, wie trendbereinigtes, Q-Q-Diagramm eignet sich am besten für eine visuelle Überpürfung der erwarteten Normalverteilung der Merkmalsdaten. Beim Q-Q-Diagramm werden die erwarteten Normalwerte auf der Y-Achse abegtragen und die Beobachtungsdaten des Merkmals auf der X-Achse. Die schwarze Diagonale im Diagramm beschreibt die Datenpunkte, in denen die Beobachtungspunke exakt den erwarteten Normalwerten und damit der Normalverteilung entsprechen. Insofern geht es also um die Bewertung der Abweichung der sichtbaren Punkteverteilung:

Im Bereich von 122 bis 125 der Testwerte ist eine kleine Abweichung von der Diagonalen ersichtlich. Ansonsten bildet dieses Q-Q-Diagramm ein gutes Beispiel ab, um nach visueller Prüfung von der annähernden Normalverteilung der Beobachtungsdaten auszugehen.

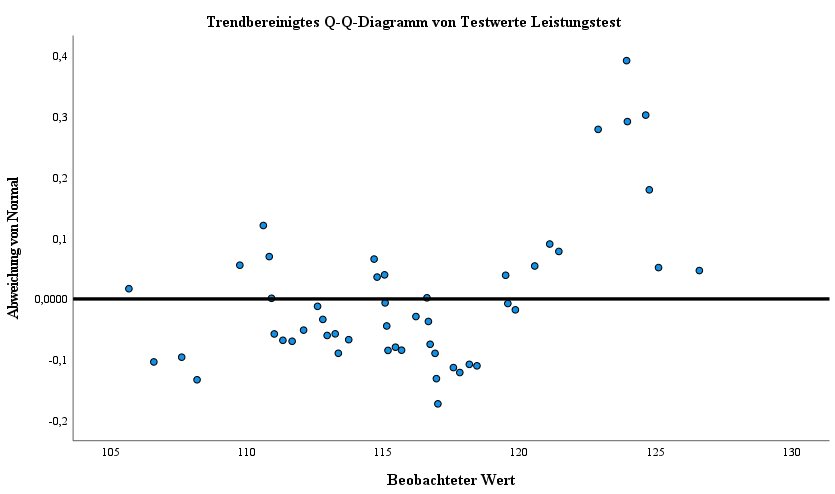
Das trendbereinigte Q-Q-Diagramm stellt die Abweichungen der Beobachtungspunkte von den erwarteten Normalwerten dar, sodass die Struktur der Abweichungen besser bewertet werden kann. Die parallele schwarze Gerade zur X-Achse beschreibt also die Punkte, die nicht von den erwarteten Normalwerten abweichen.

Ebenfalls wird hier ersichtlich, dass es im Bereich von 122 bis 125 der Testwerte zu einer deutlicheren Abweichung von der erwarteten Nullabweichung kommt (in Relation zu den restlichen Abweichungen). Man sollte allerdings darauf achten eine solche Abweichung nicht überzubewerten. Es kann also auf Basis diesen Diagramms ebenfalls von einer annähernd normalen Verteilung ausgegangen werden.

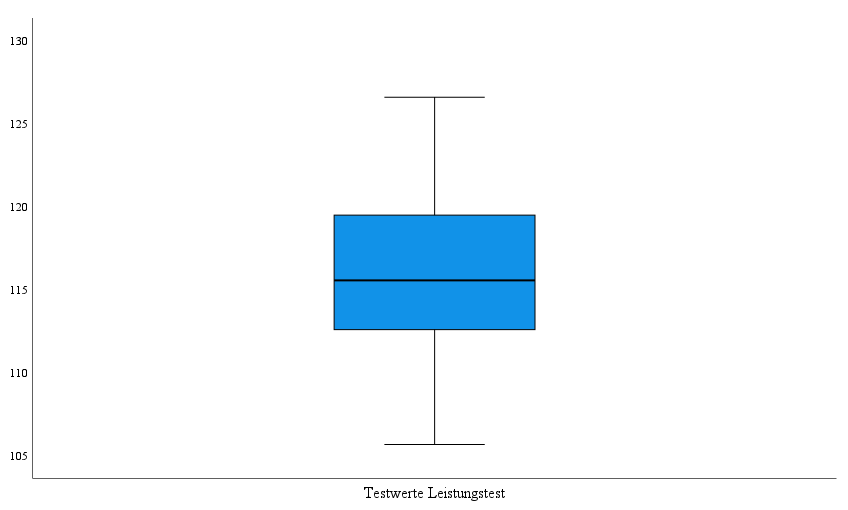
Der Boxplot als letzte Grafik der Ausgabe ist dafür geeignet mit einem Blick Ausreißer/Extremwerte zu erkennen. In den Standardeinstellung beo SPSS werden Ausreißer als leere Punkte und Extremwerte als Sternchen dargestellt. In dieser Stichprobe  gibt es keine statistisch auffälligen Werte.

Durchführung Einstichproben-t-Test

Syntax:

T-TEST
/TESTVAL=100 (fixer/erwarteter Wert)
/MISSING=ANALYSIS
/VARIABLES=v_1 (Variablenname)
/CRITERIA=CI(.95).

SPSS-Menü:

Menü -> Analysieren -> Mittelwerte vergleichen -> t-Test bei einer Stichprobe…

Nachdem die Auswahl getroffen worden ist, werden die Berechnung nach einem Klick auf die Schaltfäche „OK“ ausgeführt. Darauf zeigt sich im Ausgabefenster folgender Inhalt:

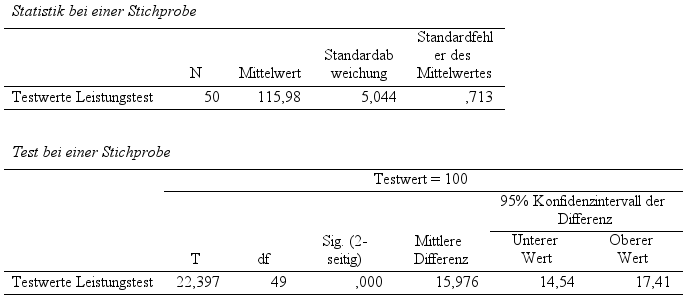
Wie gewöhnlich gibt SPSS zunächst eine Tabelle mit deskriptiven Statistiken aus (Bspw. N, M, SD, SE). Darauf die Ergebnisse der eigentlichen Testberechnungen. In der Spalte „Sig. (2-seitig)“ wird der Signifikanzwert ausgegeben. In diesem Fall der kleinste Wert, der von SPSS noch dargestellt wird, nämlich „.000“. Verbleibt man mit der Maus nach einem Doppelklick über dieser Angabe, wird der tatsächliche Wert angezeigt. Der exakte p-Wert ist in diesem Beispiel 2.15*e^-27. Also ein Wert mit insgesamt 27 Nullen vor 2.15
(= 0.00000000000000000000000000215).

Effektstärke

Neben dem wahrscheinlichkeitsbasierten Ergebnis, kann zusätzlich die Effektstärke berechnet werden. Diese ermöglicht eine differenziertere Einschätzung über das Testergebnis. Die Effektstärke wird automatisch von SPSS mit ausgegeben:

Somit zeigt das Ergebnis der Effektstärkeberechnung (d = 3.12) einen deutlichen Effekt – nach Cohen ist dies als großer Effekt zu interpretieren.

Über das 95%-Konfidenzintervall lässt sich der Schätzer in seiner Genauigkeit bewerten.

Ergebnis

Abschließend lassen sich die Ergebnisse beispielhaft ausformulieren:

Die aufgestellte Hypothese, dass Jugendliche leistungsfähiger sind als Erwachsene, überprüft mittels Einstichproben-t-Test, kann durch das vorliegende Testergebnis untermauert werden (t₍₄₉₎ = 22.40, p < .05). Jugendliche Personen weisen mit einem durchschnittlichen Testergebnis von M = 115.98 (SD = 5.04) eine höhere Leistung auf als erwachsene Personen mit einem erwarteten durchschnittlichen Testergebnis von M = 100. Der aufgedeckte Effekt von d = 3.12 (95%-KI = [2.44, 3.79] – Hedges‘ Korrektur), kann nach Cohen (1988) als großer Effekt beschrieben werden.

Literatur

• Bortz & Schuster, 2010
• Ratcliffe, 1968
• Cohen, 1988