Einführung

Die Annahme von normalen Daten ist in der Inferenzstatistik ein zentraler Sachverhalt. So spiegelt diese Annahme die Grundlage der parametrischen Verfahren wider. Dies liegt im zentralen Grenzwertsatz begründet. Für viele zunächst verwirrend ist der Umstand, dass der zentrale Grenzwertsatz keine Aussage über die erhobenen Daten selbst macht, sondern über die dahinterliegende Stichprobenkennwertverteilung. Er besagt, dass eine Stichprobenkennwertverteilung bei unabhängig und identisch erhobenen Daten asymptotisch normalverteilt ist. Die Verteilung der Daten selbst ist davon unberührt. Dieser Umstand wird nachvollziehbar, da in den meisten Fällen vor bzw. zum Zeitpunkt der Erhebung keine Kenntnis über die tatsächliche Verteilung der Daten vorliegt.

Im Großteil der Literatur wird eine Stichprobengröße von n > 30 empfohlen, ab der man von einer annähernd normalverteilten Stichprobenkennwertverteilung ausgehen kann. Hier wird ein Kompromiss zwischen verschiedenen Verteilungen eingegangen, die Stichprobendaten zugrunde liegen können (und stillschweigend voraussgesetzt, dass es sich um eine möglichst symmetrischer Verteilung handelt). Darüber hinaus empfehlen Ratcliffe (1968) bei einer leicht schiefen Verteilung eine Stichprobengröße von mindestens 50. Ist die Verteilung sehr schief, sollte sie mindestens 80 betragen.

Es sollte somit nicht missverstänlicherweise davon ausgegenagen werden, dass ab einer Stichprobengröße von n > 30, die Daten selbst annähernd normalverteilt sind!

Möchte man nun nicht mit dem zentralen Grenzwerttheorem argumentieren oder hat eine zu kleine Stichprobe, so bietet SPSS die Möglichkeit einer Überprüfung auf Normalverteilung.

Pürfung auf Normalverteilung

• Shapiro-Wilk-Test
• Kolmogorov-Smirnov-Test
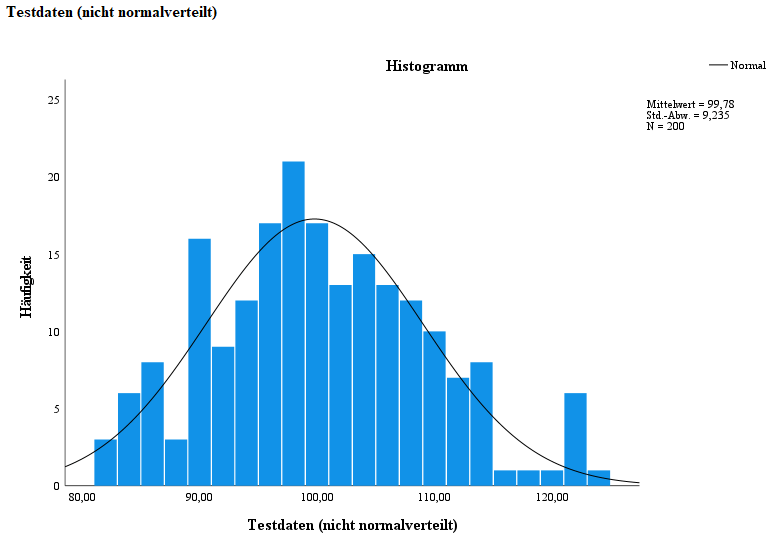
• Histogram
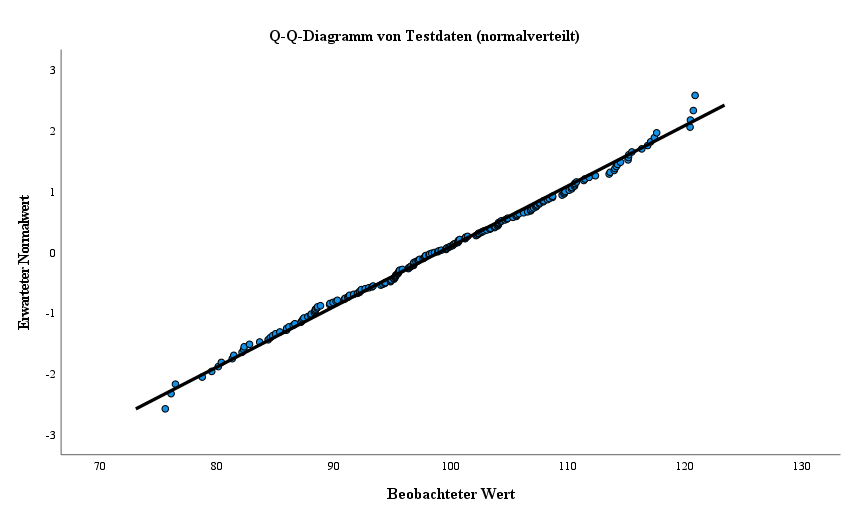
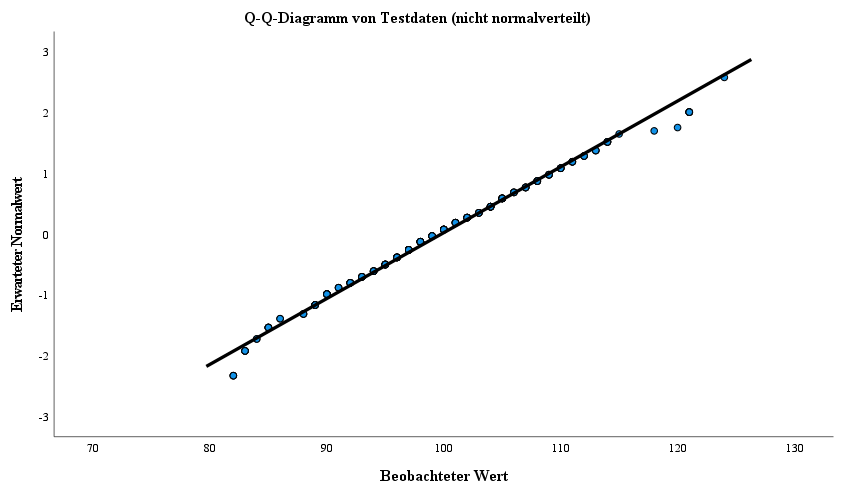
• Q-Q-Diagramm

Grundsätzlich ist die Überprüfung der Normalverteilung mittels Test begrüßenswert, da sich diese nach objektiven Maßstäben richtet. Allerdings sollten die Testergebnisse gerade bei großen Stichproben nicht alleine zur Urteilsbildung herangezogen werden. Es wird dringend empfohlen mit grafischen Mitteln wie dem Histogram oder einem Q-Q-Diagramm das Testergebnis kritisch zu hinterfragen. Der Grund dahinter verbirgt sich in der hohen Sensibilität der Testverfahren gegenüber Ausreißern bei großen Stichproben. Diese erhalten bei entsprechend großen Stichproben ein überbewertetes (unangemessenes) Gewicht, sodass es häufig zu fälschlichen Ablehnung der Nullhypothese kommt. Ferner wird in der Literatur dem Shapiro-Wilk-Test der Vorzug gegenüber dem Kolmogorov-Smirnov-Test ausgesprochen. Hier können als Anhaltspunkte von n < 5000 vor allem aber bei n < 100 genannt werden.

Die Nullhypothese als „Wunschhypothese“ – hier erläutern Bortz und Schuster (2010), weshalb es sinnvoll ist das Signifianzniveau statt der konventionellen 5% auf beispielsweise 25 % zu setzen. Beim Testen hin zur Nullhypothese gilt es sich gegen den Fehler 2. Art abzusichern, um nicht fälschlicherweise von einer normalverteilten Grundgesamtheit auszugehen, obwohl diese gar nicht der Fall ist. Ohne spezifizierte Alternativhypothese, ist die Kontrolle des Fehlers 2. Art nicht möglich, sodass diese indirekt erfolgen kann, in dem das Signifikanzniveau auf 25 % festgesetzt wird. Es wird also angenommen, dass der Fehler 2. Art bei einer Wahrscheinlichkeit von 25 % hinreichend klein wird.

Da die Überprüfung der Normalverteilung von Stichprobendaten per Augenmaß etwas Übung bedarf, werden nachfolgend drei Beispiele mit unterschiedlicher Verteilung diskutiert.

Download Beispiel-Datei: Normalverteilung.

Syntax:

EXAMINE VARIABLES=v_1 (Variablenname)
/PLOT BOXPLOT HISTOGRAM NPPLOT
/COMPARE GROUPS
/STATISTICS NONE
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.

SPSS-Menü:

Menü -> Analysieren -> Deskriptive Statistiken -> Explorative Datenanalyse…

Nach je einem Klick auf „Weiter“ und „OK“ erscheinen im Ausgabefenster folgende Ergebnisse:

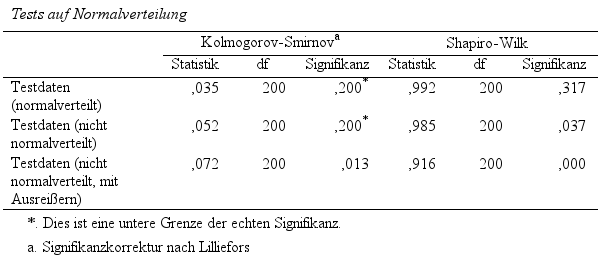
Beginnend mit den Ergebnissen von Kolmogorov-Smirnov- und Shapiro-Wilk-Tests, werden mit Blick auf die Spalte „Signifikanz“ des Shapiro-Wilk-Tests von SPSS die p-Werte ausgegeben. Mit einem Niveau von 25 %,

H₀: Das Merkmal ist (in der Grundgesamtheit) annähernd normalverteilt.

H₁: Das Merkmal weicht (in der Grundgesamtheit) von einer Normalverteilung ab.

kann die Nullhypothese im ersten Fall beibehalten werden. Somit ist die Voraussetzung normalverteilter Daten gegeben. Für letztere beiden Testvariablen gilt dies jedoch nicht.

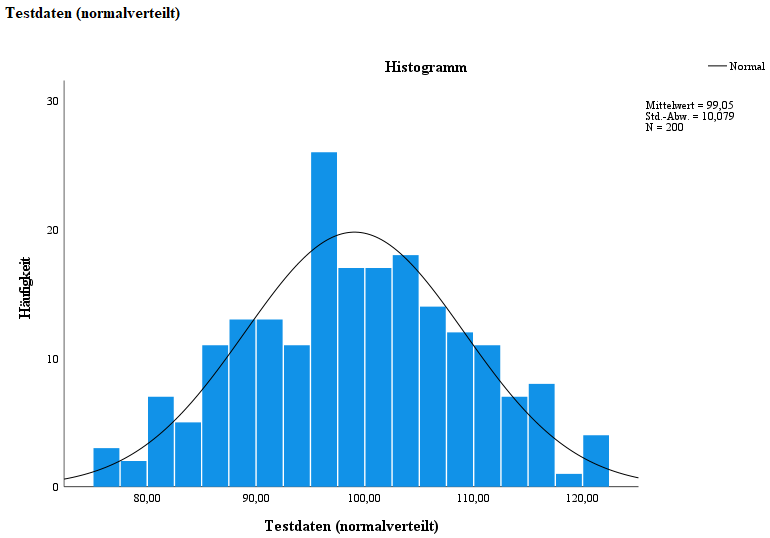
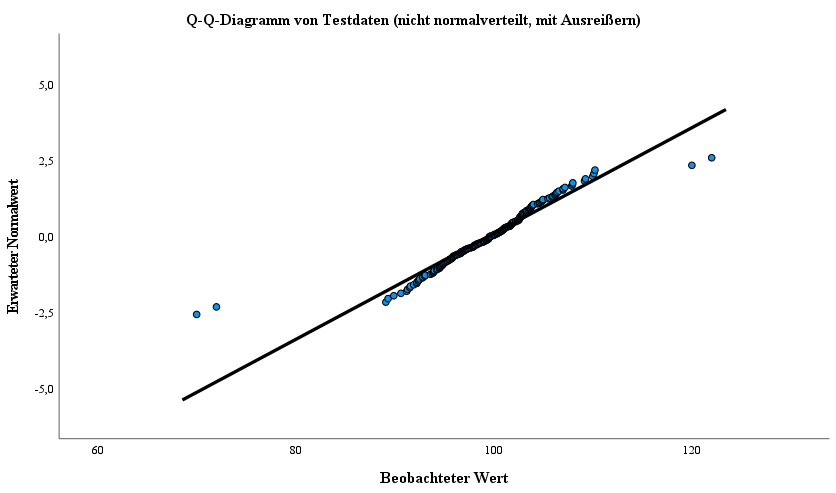
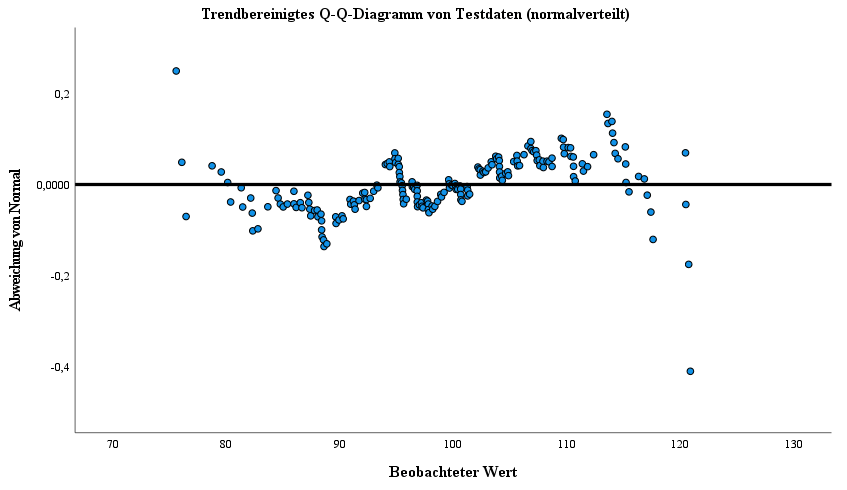
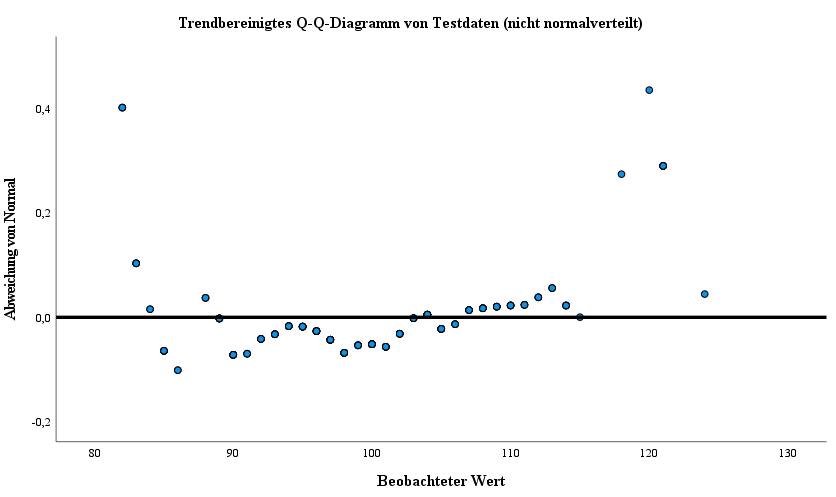
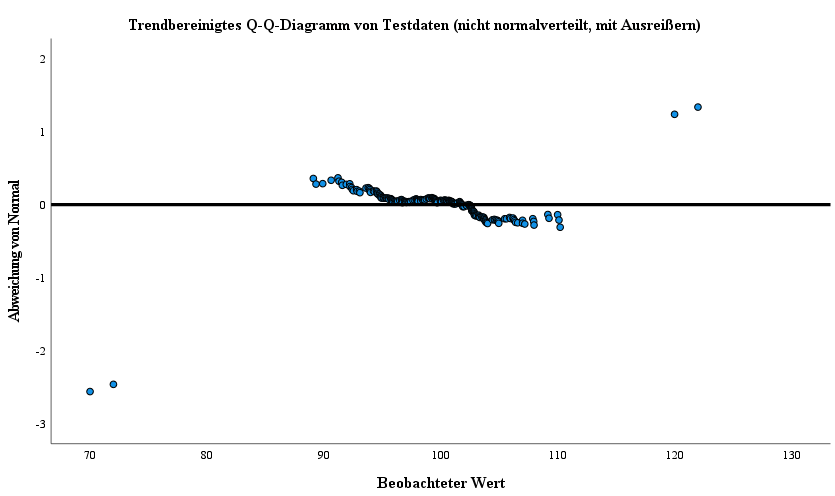
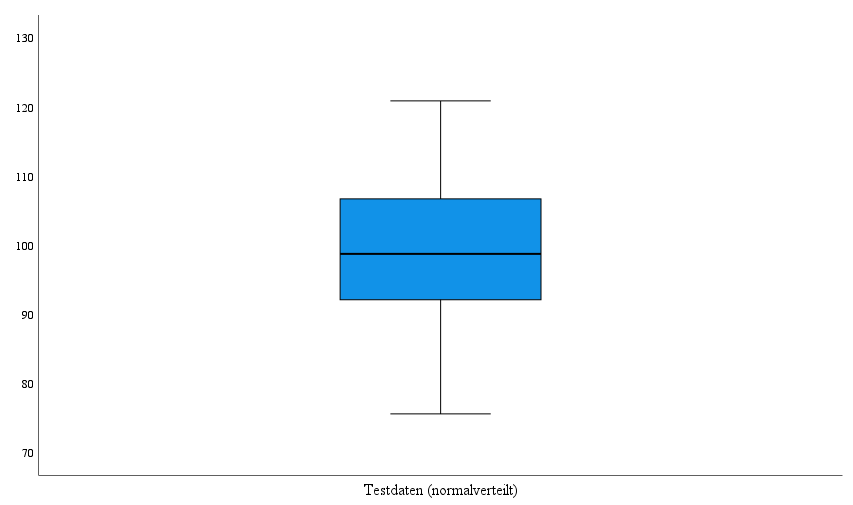
In den nachfolgenden Spalten können die Verteilungen visuell auf eine Normalverteilung der Testvariablen sowie Ausreißer hin begutachtet werden.
Dabei entspricht die erste Spalte den Ergebnissen der ersten Tesvariable, welche durch den Hypothesentest eine normale Verteilung bescheinigt wird.
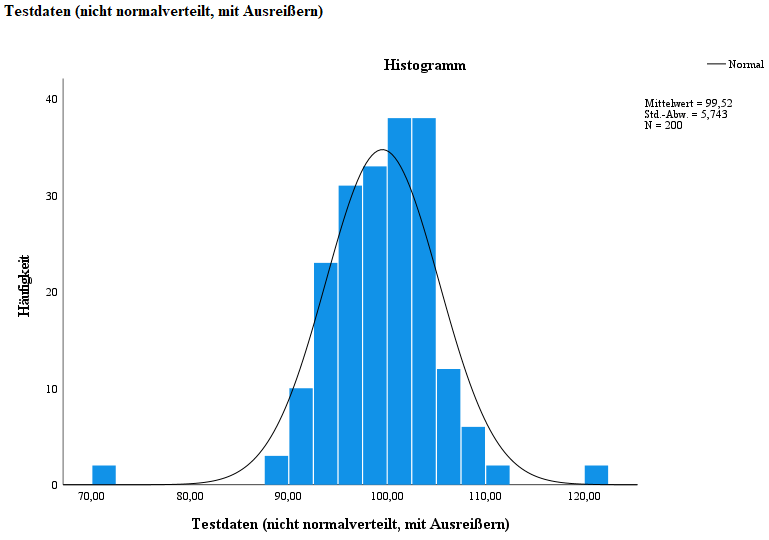
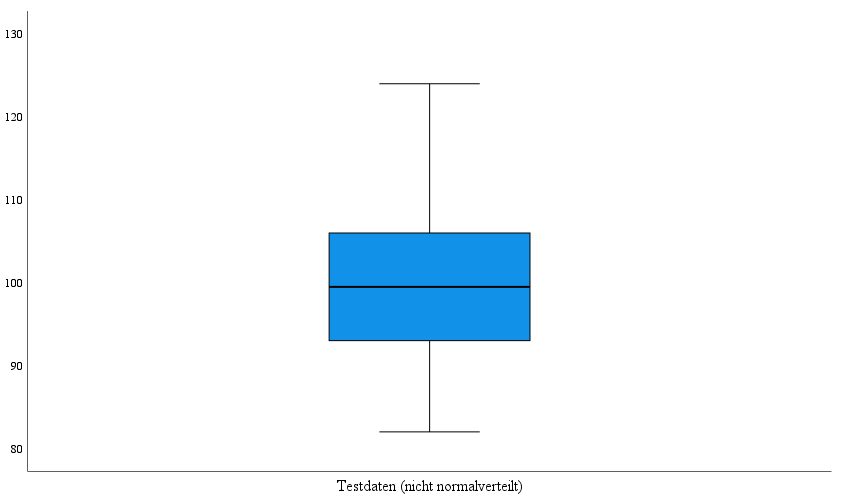
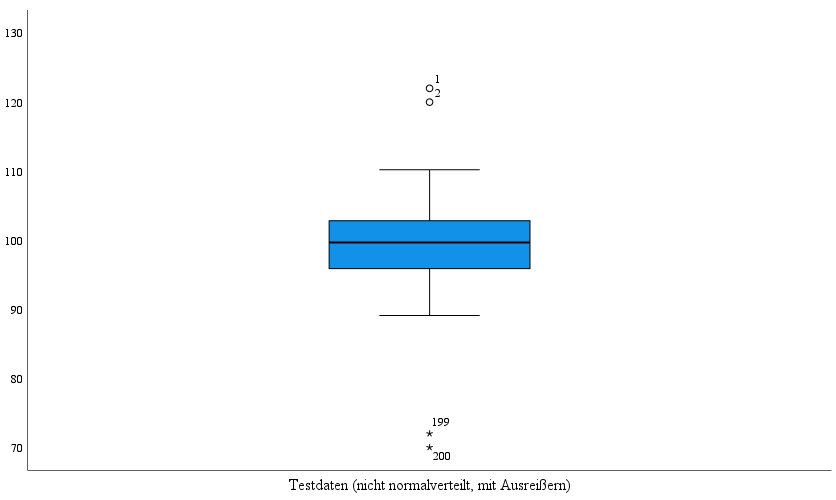
Die mittlere Spalte ist der zweiten Testvariable und die dritte Spalte der dritten Testvariable zugehörig. In dieser letzten Spalte lässt sich die Abweichung einer normalen Verteilung, bedingt durch Ausreißer, gut beobachten.

Literatur

Bortz & Schuster, 2010
Field, 2018